• 16 Nov, 2018

    算法导论 笔记4 5.2-指示器随机变量

    看完之后, 还一时不能熟练理解和应用

    5.2-1

    正好雇一次的概率是, 最优秀的人出现在第一个的概率, 就是 1/n

    雇佣n次的概率是, 所有人正好按从弱到强来面试的概率, 是 1/n!

    5.2-2

    比如有n个面试者, 第一个出现的肯定要被录取, 设第一个的能力排名是i . 那后面的n-1个人里面, 第 i+1 名之后的这些人, 怎么出现都无所谓, 因为他们肯定不会被录取了. 就看排名在 i 之前的这些人, 一共有 i-1 个人, 他们需要满足且仅需要满足: 排名第1的那个人最先出现, 概率是 1/(i-1)

    所以如果第一个人是第2名(概率是1/n), 那么后面录取一个人概率是 1/1,
    如果第一个人是第3名(概率是1/n), 那么后面录取一个人概率是 1/2
    如果第一个人是第4名(概率是1/n), 那么后面录取一个人概率是 1/3
    …
    如果第一个人是第n名(概率是1/n), 那么后面录取一个人概率是 1/(n-1)

    所以总的概率是 (1+1/2+1/3+…+1/(n-1))/n

    我们来模拟一下吧, 看看这个结果对不对.

    写一个go的程序, 来输出一下理论上的概率值, 以及模拟出来的”真实”概率. (概率乘了人数 n 然后输出的, 为了和后面提到的欧拉公式做验证)

    package main

import (
	"flag"
	"fmt"
	"math/rand"
	"time"
)

func P(n int) float32 {
	var s float32 = 0.0
	for i := 2; i <= n; i++ {
		s += 1 / float32(i-1)
	}
	return s / float32(n)
}

func interview(candidates []int) int {
	var (
		best            = 0
		hire_loop_count = 0
	)
	for _, c := range candidates {
		if c > best {
			best = c
			hire_loop_count++
		}
	}
	return hire_loop_count
}

func generate_candidates(n int) []int {
	var (
		candidates = make([]int, 0)
		exist      = make(map[int]bool)
		candidate  int
	)
	for len(candidates) < n {
		candidate = rand.Intn(5*n) + 1
		if _, ok := exist[candidate]; ok {
			continue
		} else {
			exist[candidate] = true
			candidates = append(candidates, candidate)
		}
	}
	return candidates
}

var (
	loop_count int
	N          int
)

func init() {
	rand.Seed(time.Now().Unix())

	flag.IntVar(&loop_count, "loop-count", 100, "")
	flag.IntVar(&N, "N", 100, "")
	flag.Parse()
}
func main() {

	// theory
	for n := 2; n < N; n++ {
		p := P(n)
		fmt.Printf("%d %f %f\n", n, p, p*float32(n))
	}
	return

	// real
	var candidates []int
	for n := 2; n <= N; n++ {
		c := 0
		for i := 0; i < loop_count; i++ {
			candidates = generate_candidates(n)
			if interview(candidates) == 2 {
				c++
			}
		}
		fmt.Printf("%d %d %f\n", n, c, float32(c)/float32(loop_count)*float32(n))
	}
}

    然后用python+plt把图画出来看一下.

    import matplotlib.pyplot as plt
import math

X_REAL = []
Y_REAL = []
for l in open('real.txt').readlines():
    l = l.strip()
    if l:
        x, _, y = l.split()
        x, y = int(x), float(y)
        X_REAL.append(x)
        Y_REAL.append(y)

X_THEORY = []
Y_THEORY = []
for l in open('theory.txt').readlines():
    l = l.strip()
    if l:
        x, _, y = l.split()
        x, y = int(x), float(y)
        X_THEORY.append(x)
        Y_THEORY.append(y)

X_Euler = range(2, len(X_THEORY)+2)
Y_Euler = [math.log(x-1) + 0.577 + 1/2/(x-1) for x in X_Euler]

plt.plot(X_REAL, Y_REAL, 'g', X_THEORY , Y_THEORY, 'rs', X_Euler, Y_Euler, 'b^')
plt.show()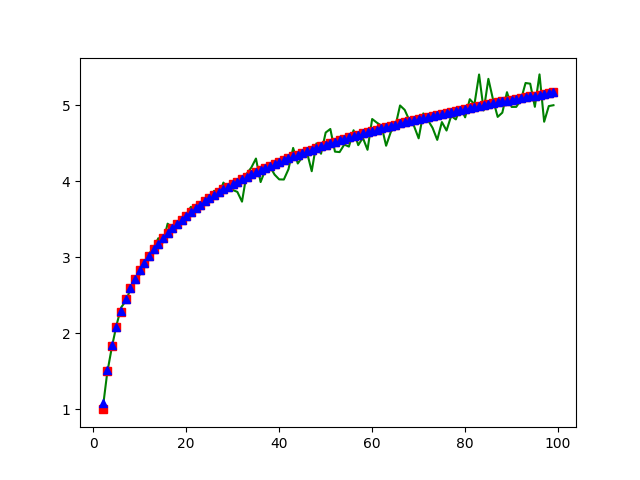

    5.2.2

    绿色是真实的数据, 红色是理论数据(1+1/2+…+1/(n-1))算出来的, 蓝色是欧拉公式算出来的. 还是符合的不错的. 欧拉公式参考https://zh.wikipedia.org/wiki/调和级数

    题外.

    因为最近在看机器学习, 感觉这个是一个可以用来学习的例子, 拿tensorflow来学习一下”真实概率”的数据, 看看学习效果怎么样.

    from __future__ import print_function
import tensorflow as tf
import numpy as np

X = []
Y = []
for l in open('real.txt').readlines():
    l = l.strip()
    if l:
        x, _, y = l.split()
        x, y = float(x), float(y)
        X.append(x)
        Y.append(y)

X = tf.cast(np.array(X), tf.float32)
Y = tf.cast(np.array(Y), tf.float32)

# Weights_1 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
# Weights_2 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
Weights_3 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
biases = tf.Variable(tf.zeros([1]))

# y = Weights_1*X*X + Weights_2*X + biases + Weights_3 * tf.math.log(X)
y = biases + Weights_3 * tf.math.log(X)

loss = tf.reduce_mean(tf.square(y-Y))
# optimizer = tf.train.GradientDescentOptimizer(0.000001)
optimizer = tf.train.AdamOptimizer(0.75)
train = optimizer.minimize(loss)


with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)

    for step in range(100000):
        sess.run(train)
        if step % 100 == 0:
            print(step, sess.run(Weights_3), sess.run(biases), sess.run(loss))

    个人感觉效果还算可以吧.

    5.2-3

    n*(1+2+3+4+5+6)/6

    我觉得这个使用指示器变量的想法是很自然的, 反而一般人不会使用”正统”的方法去计算, 所以正统方法就是, n个0的概率0 + n-1个0和1个1的概率1 + … + n个6的概率*6n

    5.2-4

    每个人拿到自己帽子的概率是 1/n , 所以期望是 1

    5.2-5

    看第i个数字, 前面有i-1个数字, 每一个比i大的概率是1/2, 所以i前面比i大的数字的个数期望是 (i-1)/2 , 那对i从1取到n, 得到题目答案应该是 西格玛(i-1)/2 i从1到n

    验证下看吧.

    package main

import (
	"fmt"
	"math/rand"
	"time"
)

func generate_nums(n int) []int {
	rand.Seed(time.Now().UnixNano())
	var (
		nums  = make([]int, 0)
		exist = make(map[int]bool)
		num   int
	)
	for len(nums) < n {
		num = rand.Intn(n)
		if _, ok := exist[num]; ok {
			continue
		} else {
			exist[num] = true
			nums = append(nums, num)
		}
	}
	return nums
}

func inversion_count(nums []int) int {
	var count = 0
	for i, n1 := range nums {
		for _, n2 := range nums[:i] {
			if n1 < n2 {
				count++
			}
		}
	}
	return count
}

func theory(n int) float32 {
	var s float32 = 0.0
	for i := 1; i <= n; i++ {
		s += float32(i-1) / 2
	}
	return s
}

func main() {
	var (
		N     = 100
		count = 1000
	)

	total := 0
	for i := 0; i < count; i++ {
		nums := generate_nums(N)
		inversion_count := inversion_count(nums)
		total += inversion_count
	}
	fmt.Printf("%f %f\n", theory(N), float32(total)/float32(count))
}

    % go run 5.2.5.go
2475.000000 2463.620117
  • 10 Nov, 2018

    算法导论 笔记3 5.1-雇佣问题

    5.1-1

    我是看的中文版本, 我觉得这个翻译的不对, 应该是说满足全序关系. 首先要理解什么是全序关系的集合, 这是一个严格的数学定义. 参考https://zh.wikipedia.org/wiki/全序关系

    全序关系即集合 X 上的反对称的、传递的和完全的二元关系

    还有一点就是, ‘在第四行的代码中, 总能决定哪一个应聘者最佳’, 不是说’运行一次这个代码, 第四行的代码都可以决定哪个最佳’ , 而是说不管如何随机, 不管如何打乱应聘者顺序, 运行多次, 乃至无数次, 第四行的代码都可以决定哪个最佳. 如果不这么理解, 全序关系就正明不了.

    我不知道怎么算是严格的数学意义上的证明, 简单说一下吧.

    反对称性, 若 a>=b && b>=a, 则 a==b . 关于反对称性, 我觉得, 还有另外一个翻译不准确的地方, ‘总能决定哪一个应聘者最佳’, 是说两两比较总能区分哪一个更好, 不能出现一样好的情况. 如果单看代码的话, 是有可能出现 a == b 的. 如果所有应聘者都是能力相同, 那么反对称性就满足不了了. 按自我纠正后的理解呢, 可以用反证法证明: 如果不满足反对称, 则A和B就不是’总能区分哪一个更好’, 所以一定满足反对称性.

    传递性, 这个真不知道怎么算’证明’, A比B好, B比C好, A’明显’比C好, 这个需要证明吗?

    完全性, a<=b, 或者 b<=a . 既然’总能区分哪一个更好’, 说明a和b总有一个比另外一个好. 用反证更好理解: 如果不满足完全性, 就是说a和b不能比较哪个更好, 这样就不能保证’总能区分哪一个更好’, 所以一定要满足完全性.

    5.1-2

    这个问题我想了好几天, 终于没想出来一个可靠的好办法, 网上搜索了别人的回答, 和我的一样不算可靠, 看来只能这样了.

    先说下我的思路.

    1. 假设已有 rand(1, n), 返回 1-n 之间随机一个数字. 这里的n是所有2的整数次方, 2, 4, 8, 16 … 1024 …
    2. 求 rand(1, x), 只需要按下面这样, 先找一个比x大的n r = rand(1, n) while r > x: r = rand(1, n) return r
    3. 现在的问题就是假设1 能不能实现, 怎么实现. 这个很简单. rand(1, 2*n) = rand(1, n) * rand(1, 2)

    网上看到的回答, 基本原理是一样的, 但合在一步里面了, 并不需要先求 rand(1, n)

    对于 rand(1, x), 先找一个最小的n,使 pow(2,n) >= x, 比如求 rand(1,5), 则取 n=3 , 然后

    r = x + 1
while r > n {
	r = 0
	for i = 1; i <= n; i++ {
		r = 2*r + rand(0,1)
	}
}
return n

    我说他不可靠, 是因为这个 while r > x 的条件可能永远达成不了, 最坏时间复杂度应该是无限大吧, 但还是可以计算一下平均时间复杂度. 我算下来, 平均时间复杂度是 O(n), 这里的n不是x, 就是上面描述里面的n. 精确的说, 平均运行时间是2n

    计算方式如下:

    首先呢, 如果x正好是2的某整数次方, 那么不会死循环, 一次过! 坏情况是x正好是2的某整数次方+1, 这种情况下, 一次过的概率只有1/2, 还有1/2的概率需要重新再来一次.

    设期望运行时间, 也就是 r = 2*r + rand(0,1) 这行代码的运行次数的期望, 为 f(n), 那么 f(n) = 1/2 * n + 1/2 * (1+f(n)) , 求得 f(n) = 2n

    写了个程序验证了一下运行时间

    # -*- coding: utf-8 -*-

import random
import time
import sys
import math

count = 0

def f(x, n):
    global count
    r = x + 1
    while r >= x:
        r = 0
        for _ in range(n):
            count += 1
            r = 2*r + random.randint(0, 1)
    return r

if __name__ == '__main__':
    x = int(eval(sys.argv[1]))
    n = int(math.ceil(math.log(x, 2)))
    print x,n

    for _ in range(10000):
        f(x, n)

    print count/10000.0

    运行结果

    % python a.py "2**9+1"
513 10
20.14

% python a.py "2**19+1"
524289 20
40.038

    5.1-3

    # -*- coding: utf-8 -*-

import sys
import random

count = 0


def fp(p=float(sys.argv[1])):
    if random.random() <= p:
        return 0
    return 1


def f2():
    global count
    while True:
        count += 1
        x = fp() - fp()
        if x == 1:
            return 0
        if x == -1:
            return 1


if __name__ == '__main__':
    for _ in range(100000):
        f2()
    print count / 100000.0

    运行结果:

    % python a.py 0.3
2.36684

% python a.py 0.5
2.00161

% python a.py 0.1
5.56982

% python a.py 0.9
5.56247

    运行时间期望分析. 函数f2中不能返回的概率是 p**2 + (1-p)**2 , 记为x, 能返回的概率则是 1-x

    设运行时间的期望是 E , 也就是代码中count的期望值(平均值).

    E = 1-x + x(1+E), 得到 E = 1/(1-x)

    另外一种计算方式

    前面提到的这种计算方式, 总觉得有些怪怪(应该是还没有形成这种思维), 有种无限递归的感觉. 所以再用另外一种方法来算一次, 拿第三个题目做例子.

    p和x的意义见上面, 记期望为E

    1. 一次就得到结果的概率是 1-x , 两次得到结果的概率是 (1-x)*x , 三次得到结果的概率是 (1-x)*x**2 , … , n次得到结果的概率是 (1-x)*x**n

    2. 所以期望 E = (1-x) + 2(1-x)x + 3(1-x)*x**2 + ... + n(1-x)*x**(n-1)

    3. 把 (1-x) 去掉, 记 S = 1 + 2x + 3x**2 + ... + n*x**(n-1) ,

    4. 两边乘x, 得 xS = x + 2x**2 + 3x**3 + n*x**n ,

    5. 两个等式想减, 得到 S-xS = 1 + x + x**2 + x**3 + ... + x**(n-1) - n*x**n

    6. 记 f = 1 + x + x**2 + x**3 + ... + x**(n-1), 两边各乘 x, 得 xf = x + x**2 + x**3 + ... + x**n , 两个等式两边相减, 得到 f-xf = 1-x**n , 所以 f=(1-x**n)/(1-x) . 因为 x < 1, 而且 n 趋向于无穷大, 所以 x**n = 0 , 所以 f=1/(1-x)

    7. 根据5和6, 得到 S-xS = 1/(1-x) - n*x**n = 1/(1-x) 所以 `S = 1/(1-x)**2’

    8. 将7代入2, 得到期望 E = 1/(1-x)

  • 9 Nov, 2018

    算法导论 笔记2 4.2-矩阵乘法Strassen算法

    4.2.1 使用Strassen计算

    [1 3][6 8]
[7 5][4 2]

    先手工算一下答案记下来

    [18 14]
[62 66]

    完全参考书的步骤来做一下这个题目

    1. 分解矩阵 略

    2. 创建并计算10个矩阵

         S1 = B12 - B22 = [6]
   S2 = A11 + A12 = [4]
   S3 = A21 + A22 = [12]
   S4 = B21 - B11 = [-2]
   S5 = A11 + A22 = [6]
   S6 = B11 + B22 = [8]
   S7 = A12 - A22 = [-2]
   S8 = B21 + B22 = [6]
   S9 = A11 - A21 = [-6]
   S10 = B11 + B12 = [14]

    3. 计算7次矩阵乘法

       P1 = A11 * S1 = [6]
 P2 = S2 * B22 = [8]
 P3 = S3 * B11 = [72]
 P4 = A22 * S4 = [-10]
 P5 = S5 * S6 = [48]
 P6 = S7 * S8 = [-12]
 P7 = S9 * S10 = [-84]

    4. 计算 C11 C12 C21 C22

       C11 = P5 + P4 - P2 + P6 = [18]
 C12 = P1 + P2 = [14]
 C21 = P3 + P4 = [62]
 C22 = P5 + P1 - P3 - P7 = [66]

    没有纸笔, 靠我的脑子想不出来, 我先跳到第五章吧.

  • 30 Oct, 2018

    算法导论 读书笔记1

    先占个坑, 督促自己一下.

    2018-11-04T19:55:28+0800

    4.1.1

    返回数组里面的最大值, 例子参见下面的 4.1.2

    4.1.2

    def find_maximum_subarray(A):
    maximum_subarry_sum = None
    rst = (None, None)
    for i in range(len(A)):
        sum_of_array_i_to_j = 0
        for j in range(i, len(A)):
            sum_of_array_i_to_j += A[j]
            if sum_of_array_i_to_j > maximum_subarry_sum:
                maximum_subarry_sum = sum_of_array_i_to_j
                rst = (i, j)

    return rst


if __name__ == '__main__':
    A = [13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7]
    i, j = find_maximum_subarray(A)
    print(A[i: j+1])

    import random
    A = []
    for i in range(30):
        A.append(random.randint(-100, -1))

    print(A)
    i, j = find_maximum_subarray(A)
    print(A[i: j+1])

    4.1.3

    代码如下, 在我电脑测试时, 临界点为45. 当数组长度小于45时, 采用暴力算法, 显然不会改变性能交叉点. 但比如说, 当数组长度小于10时采用暴力算法, 可以改变性能交叉点.

    # -*- coding: utf-8 -*-


def find_maximum_subarray_1(A, low, high):
    """
    暴力运算
    """
    maximum_subarry_sum = None
    rst = (None, None)
    for i in range(low, high+1):
        sum_of_array_i_to_j = 0
        for j in range(i, high+1):
            sum_of_array_i_to_j += A[j]
            if sum_of_array_i_to_j > maximum_subarry_sum:
                maximum_subarry_sum = sum_of_array_i_to_j
                rst = (i, j)

    return rst[0], rst[1], maximum_subarry_sum


def find_maximum_subarray(A, low, high):
    """
    分治
    """
    if high - low <= 10:
        return find_maximum_subarray_1(A, low, high)

    mid = (low+high)/2

    left_low, left_high, left_sum = find_maximum_subarray(A, low, mid)
    right_low, right_high, right_sum = find_maximum_subarray(A, mid+1, high)

    left_sum_part, array_sum = None, 0
    for i in range(mid, low-1, -1):
        array_sum += A[i]
        if array_sum > left_sum_part:
            left_sum_part = array_sum
            max_left = i

    right_sum_part, array_sum = None, 0
    for i in range(mid+1, high+1):
        array_sum += A[i]
        if array_sum > right_sum_part:
            right_sum_part = array_sum
            max_right = i

    if left_sum_part+right_sum_part > max(left_sum, right_sum):
        return max_left, max_right, left_sum_part+right_sum_part

    if left_sum > right_sum:
        return left_low, left_high, left_sum

    return right_low, right_high, right_sum


def main():
    import time
    import random
    import sys
    A_length = int(sys.argv[1])
    A_count = int(sys.argv[2]) if sys.argv[2:] else 1000

    all_A = []
    for i in range(A_count):
        all_A.append([random.randint(-100, 100) for _ in range(A_length)])

    start_time = time.time()
    for i in range(A_count):
        find_maximum_subarray_1(all_A[i], 0, A_length-1)
    end_time = time.time()
    print(u'暴力 %.2f' % (end_time - start_time))

    start_time = time.time()
    for i in range(A_count):
        find_maximum_subarray(all_A[i], 0, A_length-1)
    end_time = time.time()
    print(u'分治 %.2f' % (end_time - start_time))


if __name__ == '__main__':
    main()

    4.1.4

    如果最终的结果maximum_subarry_sum是小于0的, 那么就返回一个空数组

    4.1.5

    个人感觉, 完全按题干中的”如下思想”来写, 时间复杂度并不是O(n), 而是O(n*2). 因为第一层需要遍历1..n, 当遍历到j的时候, 第二层最坏情况下, 需要遍历i..j.

    动态规划的话,还需要一个额外的数组, 叫它 maximum_subarry_endswith_j, 记录的是A[:j]里面以A[j]结尾的最大子数组. 能避免第二层的O(n)的复杂度. 代码如下:

    def find_maximum_subarray_2(A, low, high):
    """
    动态规划
    """

    maximum_subarry = (-1, -1, None)
    maximum_subarry_endswith_j = []

    maximum_subarry = (low, low, A[low])
    maximum_subarry_endswith_j.append((low, A[low]))

    for j in range(low+1, high+1):
        _start, _max_sum = maximum_subarry_endswith_j[-1]
        if _max_sum < 0:
            maximum_subarry_endswith_j.append((j, A[j]))
        else:
            maximum_subarry_endswith_j.append((_start, _max_sum + A[j]))

        if maximum_subarry_endswith_j[-1][1] > maximum_subarry[-1]:
            maximum_subarry = (maximum_subarry_endswith_j[-1][0], j, maximum_subarry_endswith_j[-1][1])

    return maximum_subarry

    数组长度100, 跑1000个100长度的随机的数组, 时间如下:

    % python c.py 100 1000
暴力 0.71
分治 0.23
动态规划 0.06


% python c.py 200 1000
暴力 2.57
分治 0.48
动态规划 0.11

% python c.py 400 1000
暴力 10.25
分治 1.08
动态规划 0.23
  • 27 Sep, 2018

    nginx配置中的if条件与querystring配置例子 

    set $search 0;
if ($request_uri ~ "_search"){
    set $search 1;
}
if ($request_uri ~ "_count"){
    set $search 1;
}

if ($arg_ignore_unavailable = true) {
    set $search "${search}1";
}
if ($search = 1) {
    set $args $args&ignore_unavailable=true;
}


if ($arg_preference = "") {
    set $args $args&preference=$upstream_http_django_user;
}
  • 20 Aug, 2018

    部署superset+clickhouse

    我选择使用docker方式安装部署, 虽然中间碰到两个坑, 但对于之后的二次部署或者多次部署,应该还是简单一些.

  • 3 Aug, 2018

    mmap中shared方式锁定的内存能否释放

    很多文章都提到 cache中的 shared memory的cache不能被释放, 比如https://linux.cn/article-7310-1.html, 那自然就有一个问题: 如果系统内存用完了, 程序继续通过share memory mmap读取数据, 会发生什么情况?

    是老的cache被释放, 还是读取失败?

    做了一下测试, 还是会释放的, 只不过不能通过 echo 3 > /proc/sys/vm/drop_caches 这种方式释放而已.

    找一个4G内存的机器做下测试.

    写了一段代码, mmap读取一个3G文件的每一页, 这样就会让文件常驻cache了. echo 3 > /proc/sys/vm/drop_caches 之后可以看到cahce没有少, vmtouch也可以看到未释放.

    然后 cat another-3G-file > /dev/null,通过 vmtouch可以看到老文件已经有page不在cache中了. 而another-3G-file几乎全部在cache.

  • 28 Jun, 2018

    golang里面array/slice的内存分配测试1

    1. 当cap还够用的时候, append不会申请新内存
    2. cap不够的时候, 会申请一块新内存. buf = append(buf, …), 新得到的buf会是一块新内存,指针是变掉的, 新的cap是之前的两倍(但一定是8的偶数倍, 比如2->8, 10->32)
    3. newbuf = buf[2:5] 生成slice的时候, newbuf指向buf[2], 他们共用同一块内存, 直到上面2中描述的新内存申请后, 他们会指向不同内存. 不管是buf还是newbuf扩容
    4. make([]byte, 10)[0:] , len, cap都是10, append会分配新内存.
    5. make([]byte, 10)[0:0] , len是0, cap是10, append 10 以内不会分配新内存
  • 13 Jun, 2018

    函数中传递指针引起的一个BUG

    我是觉得编程里面最烧脑的就是传值和传引用的甄别, 一不小心就会出错.

    我是写一个kafka lib https://github.com/childe/healer, producer的类写好了, 然后在此基础上写一个可执行文件, 从stdin输入数据, 然后写入kafka.

    简单说一下producer逻辑, 输入1000条之后做为一批数据一起写kafka, 或者是200ms定时器到了就写, 哪怕没有1000条.

    但是在测试过程中, 无意间发现, 最终写到kafka的数据是错乱的, 后面写的数据会把前面的数据覆盖掉. 比如先输入 1111111111, 再输入 2222222222, 最后写到kafka的就是两条 2222222222

    这就让人很尴尬了…

  • 8 Jun, 2018

    ES中使用mmap存储的索引会锁定内存不释放?

    在可用内存不充足的情况下, ES中索引配置如果使用mmapfs, 会导致内存不足, Load飙升.

    虽然从发现这个问题到最后确认原因,花了很长时间, 这里长话短说.