-
算法导论 笔记4 5.2-指示器随机变量
看完之后, 还一时不能熟练理解和应用
5.2-1
正好雇一次的概率是, 最优秀的人出现在第一个的概率, 就是 1/n
雇佣n次的概率是, 所有人正好按从弱到强来面试的概率, 是 1/n!
5.2-2
比如有n个面试者, 第一个出现的肯定要被录取, 设第一个的能力排名是i . 那后面的n-1个人里面, 第 i+1 名之后的这些人, 怎么出现都无所谓, 因为他们肯定不会被录取了. 就看排名在 i 之前的这些人, 一共有 i-1 个人, 他们需要满足且仅需要满足: 排名第1的那个人最先出现, 概率是 1/(i-1)
所以如果第一个人是第2名(概率是1/n), 那么后面录取一个人概率是 1/1,
如果第一个人是第3名(概率是1/n), 那么后面录取一个人概率是 1/2
如果第一个人是第4名(概率是1/n), 那么后面录取一个人概率是 1/3
…
如果第一个人是第n名(概率是1/n), 那么后面录取一个人概率是 1/(n-1)所以总的概率是 (1+1/2+1/3+…+1/(n-1))/n
我们来模拟一下吧, 看看这个结果对不对.
写一个go的程序, 来输出一下理论上的概率值, 以及模拟出来的”真实”概率. (概率乘了人数 n 然后输出的, 为了和后面提到的欧拉公式做验证)
package main import ( "flag" "fmt" "math/rand" "time" ) func P(n int) float32 { var s float32 = 0.0 for i := 2; i <= n; i++ { s += 1 / float32(i-1) } return s / float32(n) } func interview(candidates []int) int { var ( best = 0 hire_loop_count = 0 ) for _, c := range candidates { if c > best { best = c hire_loop_count++ } } return hire_loop_count } func generate_candidates(n int) []int { var ( candidates = make([]int, 0) exist = make(map[int]bool) candidate int ) for len(candidates) < n { candidate = rand.Intn(5*n) + 1 if _, ok := exist[candidate]; ok { continue } else { exist[candidate] = true candidates = append(candidates, candidate) } } return candidates } var ( loop_count int N int ) func init() { rand.Seed(time.Now().Unix()) flag.IntVar(&loop_count, "loop-count", 100, "") flag.IntVar(&N, "N", 100, "") flag.Parse() } func main() { // theory for n := 2; n < N; n++ { p := P(n) fmt.Printf("%d %f %f\n", n, p, p*float32(n)) } return // real var candidates []int for n := 2; n <= N; n++ { c := 0 for i := 0; i < loop_count; i++ { candidates = generate_candidates(n) if interview(candidates) == 2 { c++ } } fmt.Printf("%d %d %f\n", n, c, float32(c)/float32(loop_count)*float32(n)) } }然后用python+plt把图画出来看一下.
import matplotlib.pyplot as plt import math X_REAL = [] Y_REAL = [] for l in open('real.txt').readlines(): l = l.strip() if l: x, _, y = l.split() x, y = int(x), float(y) X_REAL.append(x) Y_REAL.append(y) X_THEORY = [] Y_THEORY = [] for l in open('theory.txt').readlines(): l = l.strip() if l: x, _, y = l.split() x, y = int(x), float(y) X_THEORY.append(x) Y_THEORY.append(y) X_Euler = range(2, len(X_THEORY)+2) Y_Euler = [math.log(x-1) + 0.577 + 1/2/(x-1) for x in X_Euler] plt.plot(X_REAL, Y_REAL, 'g', X_THEORY , Y_THEORY, 'rs', X_Euler, Y_Euler, 'b^') plt.show()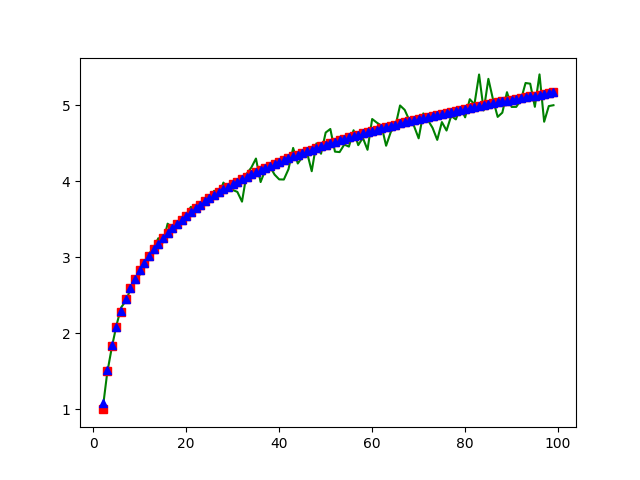
绿色是真实的数据, 红色是理论数据(1+1/2+…+1/(n-1))算出来的, 蓝色是欧拉公式算出来的. 还是符合的不错的. 欧拉公式参考https://zh.wikipedia.org/wiki/调和级数
题外.
因为最近在看机器学习, 感觉这个是一个可以用来学习的例子, 拿tensorflow来学习一下”真实概率”的数据, 看看学习效果怎么样.
from __future__ import print_function import tensorflow as tf import numpy as np X = [] Y = [] for l in open('real.txt').readlines(): l = l.strip() if l: x, _, y = l.split() x, y = float(x), float(y) X.append(x) Y.append(y) X = tf.cast(np.array(X), tf.float32) Y = tf.cast(np.array(Y), tf.float32) # Weights_1 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32) # Weights_2 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32) Weights_3 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32) biases = tf.Variable(tf.zeros([1])) # y = Weights_1*X*X + Weights_2*X + biases + Weights_3 * tf.math.log(X) y = biases + Weights_3 * tf.math.log(X) loss = tf.reduce_mean(tf.square(y-Y)) # optimizer = tf.train.GradientDescentOptimizer(0.000001) optimizer = tf.train.AdamOptimizer(0.75) train = optimizer.minimize(loss) with tf.Session() as sess: init = tf.global_variables_initializer() sess.run(init) for step in range(100000): sess.run(train) if step % 100 == 0: print(step, sess.run(Weights_3), sess.run(biases), sess.run(loss))个人感觉效果还算可以吧.
5.2-3
n*(1+2+3+4+5+6)/6
我觉得这个使用指示器变量的想法是很自然的, 反而一般人不会使用”正统”的方法去计算, 所以正统方法就是, n个0的概率0 + n-1个0和1个1的概率1 + … + n个6的概率*6n
5.2-4
每个人拿到自己帽子的概率是 1/n , 所以期望是 1
5.2-5
看第i个数字, 前面有i-1个数字, 每一个比i大的概率是1/2, 所以i前面比i大的数字的个数期望是 (i-1)/2 , 那对i从1取到n, 得到题目答案应该是 西格玛(i-1)/2 i从1到n
验证下看吧.
package main import ( "fmt" "math/rand" "time" ) func generate_nums(n int) []int { rand.Seed(time.Now().UnixNano()) var ( nums = make([]int, 0) exist = make(map[int]bool) num int ) for len(nums) < n { num = rand.Intn(n) if _, ok := exist[num]; ok { continue } else { exist[num] = true nums = append(nums, num) } } return nums } func inversion_count(nums []int) int { var count = 0 for i, n1 := range nums { for _, n2 := range nums[:i] { if n1 < n2 { count++ } } } return count } func theory(n int) float32 { var s float32 = 0.0 for i := 1; i <= n; i++ { s += float32(i-1) / 2 } return s } func main() { var ( N = 100 count = 1000 ) total := 0 for i := 0; i < count; i++ { nums := generate_nums(N) inversion_count := inversion_count(nums) total += inversion_count } fmt.Printf("%f %f\n", theory(N), float32(total)/float32(count)) }% go run 5.2.5.go 2475.000000 2463.620117 -
算法导论 笔记3 5.1-雇佣问题
5.1-1
我是看的中文版本, 我觉得这个翻译的不对, 应该是说满足
全序关系. 首先要理解什么是全序关系的集合, 这是一个严格的数学定义. 参考https://zh.wikipedia.org/wiki/全序关系全序关系即集合 X 上的反对称的、传递的和完全的二元关系还有一点就是, ‘在第四行的代码中, 总能决定哪一个应聘者最佳’, 不是说’运行一次这个代码, 第四行的代码都可以决定哪个最佳’ , 而是说不管如何随机, 不管如何打乱应聘者顺序, 运行多次, 乃至无数次, 第四行的代码都可以决定哪个最佳. 如果不这么理解, 全序关系就正明不了.
我不知道怎么算是严格的数学意义上的证明, 简单说一下吧.
反对称性, 若 a>=b && b>=a, 则 a==b . 关于反对称性, 我觉得, 还有另外一个翻译不准确的地方, ‘总能决定哪一个应聘者最佳’, 是说两两比较总能区分哪一个更好, 不能出现一样好的情况. 如果单看代码的话, 是有可能出现 a == b 的. 如果所有应聘者都是能力相同, 那么反对称性就满足不了了. 按自我纠正后的理解呢, 可以用反证法证明: 如果不满足反对称, 则A和B就不是’总能区分哪一个更好’, 所以一定满足反对称性.
传递性, 这个真不知道怎么算’证明’, A比B好, B比C好, A’明显’比C好, 这个需要证明吗?
完全性, a<=b, 或者 b<=a . 既然’总能区分哪一个更好’, 说明a和b总有一个比另外一个好. 用反证更好理解: 如果不满足完全性, 就是说a和b不能比较哪个更好, 这样就不能保证’总能区分哪一个更好’, 所以一定要满足完全性.
5.1-2
这个问题我想了好几天, 终于没想出来一个可靠的好办法, 网上搜索了别人的回答, 和我的一样不算可靠, 看来只能这样了.
先说下我的思路.
- 假设已有 rand(1, n), 返回 1-n 之间随机一个数字. 这里的n是所有2的整数次方, 2, 4, 8, 16 … 1024 …
- 求 rand(1, x), 只需要按下面这样, 先找一个比x大的n r = rand(1, n) while r > x: r = rand(1, n) return r
- 现在的问题就是假设1 能不能实现, 怎么实现. 这个很简单.
rand(1, 2*n) = rand(1, n) * rand(1, 2)
网上看到的回答, 基本原理是一样的, 但合在一步里面了, 并不需要先求 rand(1, n)
对于 rand(1, x), 先找一个最小的n,使 pow(2,n) >= x, 比如求 rand(1,5), 则取 n=3 , 然后
r = x + 1 while r > n { r = 0 for i = 1; i <= n; i++ { r = 2*r + rand(0,1) } } return n我说他不可靠, 是因为这个
while r > x的条件可能永远达成不了, 最坏时间复杂度应该是无限大吧, 但还是可以计算一下平均时间复杂度. 我算下来, 平均时间复杂度是 O(n), 这里的n不是x, 就是上面描述里面的n. 精确的说, 平均运行时间是2n计算方式如下:
首先呢, 如果x正好是2的某整数次方, 那么不会死循环, 一次过! 坏情况是x正好是2的某整数次方+1, 这种情况下, 一次过的概率只有1/2, 还有1/2的概率需要重新再来一次.
设期望运行时间, 也就是
r = 2*r + rand(0,1)这行代码的运行次数的期望, 为 f(n), 那么 f(n) = 1/2 * n + 1/2 * (1+f(n)) , 求得 f(n) = 2n写了个程序验证了一下运行时间
# -*- coding: utf-8 -*- import random import time import sys import math count = 0 def f(x, n): global count r = x + 1 while r >= x: r = 0 for _ in range(n): count += 1 r = 2*r + random.randint(0, 1) return r if __name__ == '__main__': x = int(eval(sys.argv[1])) n = int(math.ceil(math.log(x, 2))) print x,n for _ in range(10000): f(x, n) print count/10000.0运行结果
% python a.py "2**9+1" 513 10 20.14 % python a.py "2**19+1" 524289 20 40.0385.1-3
# -*- coding: utf-8 -*- import sys import random count = 0 def fp(p=float(sys.argv[1])): if random.random() <= p: return 0 return 1 def f2(): global count while True: count += 1 x = fp() - fp() if x == 1: return 0 if x == -1: return 1 if __name__ == '__main__': for _ in range(100000): f2() print count / 100000.0运行结果:
% python a.py 0.3 2.36684 % python a.py 0.5 2.00161 % python a.py 0.1 5.56982 % python a.py 0.9 5.56247运行时间期望分析. 函数f2中不能返回的概率是
p**2 + (1-p)**2, 记为x, 能返回的概率则是 1-x设运行时间的期望是 E , 也就是代码中count的期望值(平均值).
E = 1-x + x(1+E), 得到 E = 1/(1-x)
另外一种计算方式
前面提到的这种计算方式, 总觉得有些怪怪(应该是还没有形成这种思维), 有种无限递归的感觉. 所以再用另外一种方法来算一次, 拿第三个题目做例子.
p和x的意义见上面, 记期望为E
-
一次就得到结果的概率是
1-x, 两次得到结果的概率是(1-x)*x, 三次得到结果的概率是(1-x)*x**2, … , n次得到结果的概率是(1-x)*x**n -
所以期望
E = (1-x) + 2(1-x)x + 3(1-x)*x**2 + ... + n(1-x)*x**(n-1) -
把 (1-x) 去掉, 记
S = 1 + 2x + 3x**2 + ... + n*x**(n-1), -
两边乘x, 得
xS = x + 2x**2 + 3x**3 + n*x**n, -
两个等式想减, 得到
S-xS = 1 + x + x**2 + x**3 + ... + x**(n-1) - n*x**n -
记
f = 1 + x + x**2 + x**3 + ... + x**(n-1), 两边各乘 x, 得xf = x + x**2 + x**3 + ... + x**n, 两个等式两边相减, 得到f-xf = 1-x**n, 所以f=(1-x**n)/(1-x). 因为 x < 1, 而且 n 趋向于无穷大, 所以x**n = 0, 所以f=1/(1-x) -
根据5和6, 得到
S-xS = 1/(1-x) - n*x**n = 1/(1-x)所以 `S = 1/(1-x)**2’ -
将7代入2, 得到期望
E = 1/(1-x)
-
算法导论 笔记2 4.2-矩阵乘法Strassen算法
4.2.1 使用Strassen计算
[1 3][6 8] [7 5][4 2]先手工算一下答案记下来
[18 14] [62 66]完全参考书的步骤来做一下这个题目
- 分解矩阵 略
-
创建并计算10个矩阵
S1 = B12 - B22 = [6] S2 = A11 + A12 = [4] S3 = A21 + A22 = [12] S4 = B21 - B11 = [-2] S5 = A11 + A22 = [6] S6 = B11 + B22 = [8] S7 = A12 - A22 = [-2] S8 = B21 + B22 = [6] S9 = A11 - A21 = [-6] S10 = B11 + B12 = [14] -
计算7次矩阵乘法
P1 = A11 * S1 = [6] P2 = S2 * B22 = [8] P3 = S3 * B11 = [72] P4 = A22 * S4 = [-10] P5 = S5 * S6 = [48] P6 = S7 * S8 = [-12] P7 = S9 * S10 = [-84] -
计算 C11 C12 C21 C22
C11 = P5 + P4 - P2 + P6 = [18] C12 = P1 + P2 = [14] C21 = P3 + P4 = [62] C22 = P5 + P1 - P3 - P7 = [66]
没有纸笔, 靠我的脑子想不出来, 我先跳到第五章吧.
-
算法导论 读书笔记1
先占个坑, 督促自己一下.
2018-11-04T19:55:28+0800
4.1.1
返回数组里面的最大值, 例子参见下面的 4.1.2
4.1.2
def find_maximum_subarray(A): maximum_subarry_sum = None rst = (None, None) for i in range(len(A)): sum_of_array_i_to_j = 0 for j in range(i, len(A)): sum_of_array_i_to_j += A[j] if sum_of_array_i_to_j > maximum_subarry_sum: maximum_subarry_sum = sum_of_array_i_to_j rst = (i, j) return rst if __name__ == '__main__': A = [13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7] i, j = find_maximum_subarray(A) print(A[i: j+1]) import random A = [] for i in range(30): A.append(random.randint(-100, -1)) print(A) i, j = find_maximum_subarray(A) print(A[i: j+1])4.1.3
代码如下, 在我电脑测试时, 临界点为45. 当数组长度小于45时, 采用暴力算法, 显然不会改变性能交叉点. 但比如说, 当数组长度小于10时采用暴力算法, 可以改变性能交叉点.
# -*- coding: utf-8 -*- def find_maximum_subarray_1(A, low, high): """ 暴力运算 """ maximum_subarry_sum = None rst = (None, None) for i in range(low, high+1): sum_of_array_i_to_j = 0 for j in range(i, high+1): sum_of_array_i_to_j += A[j] if sum_of_array_i_to_j > maximum_subarry_sum: maximum_subarry_sum = sum_of_array_i_to_j rst = (i, j) return rst[0], rst[1], maximum_subarry_sum def find_maximum_subarray(A, low, high): """ 分治 """ if high - low <= 10: return find_maximum_subarray_1(A, low, high) mid = (low+high)/2 left_low, left_high, left_sum = find_maximum_subarray(A, low, mid) right_low, right_high, right_sum = find_maximum_subarray(A, mid+1, high) left_sum_part, array_sum = None, 0 for i in range(mid, low-1, -1): array_sum += A[i] if array_sum > left_sum_part: left_sum_part = array_sum max_left = i right_sum_part, array_sum = None, 0 for i in range(mid+1, high+1): array_sum += A[i] if array_sum > right_sum_part: right_sum_part = array_sum max_right = i if left_sum_part+right_sum_part > max(left_sum, right_sum): return max_left, max_right, left_sum_part+right_sum_part if left_sum > right_sum: return left_low, left_high, left_sum return right_low, right_high, right_sum def main(): import time import random import sys A_length = int(sys.argv[1]) A_count = int(sys.argv[2]) if sys.argv[2:] else 1000 all_A = [] for i in range(A_count): all_A.append([random.randint(-100, 100) for _ in range(A_length)]) start_time = time.time() for i in range(A_count): find_maximum_subarray_1(all_A[i], 0, A_length-1) end_time = time.time() print(u'暴力 %.2f' % (end_time - start_time)) start_time = time.time() for i in range(A_count): find_maximum_subarray(all_A[i], 0, A_length-1) end_time = time.time() print(u'分治 %.2f' % (end_time - start_time)) if __name__ == '__main__': main()4.1.4
如果最终的结果maximum_subarry_sum是小于0的, 那么就返回一个空数组
4.1.5
个人感觉, 完全按题干中的”如下思想”来写, 时间复杂度并不是O(n), 而是O(n*2). 因为第一层需要遍历1..n, 当遍历到j的时候, 第二层最坏情况下, 需要遍历i..j.
动态规划的话,还需要一个额外的数组, 叫它 maximum_subarry_endswith_j, 记录的是A[:j]里面以A[j]结尾的最大子数组. 能避免第二层的O(n)的复杂度. 代码如下:
def find_maximum_subarray_2(A, low, high): """ 动态规划 """ maximum_subarry = (-1, -1, None) maximum_subarry_endswith_j = [] maximum_subarry = (low, low, A[low]) maximum_subarry_endswith_j.append((low, A[low])) for j in range(low+1, high+1): _start, _max_sum = maximum_subarry_endswith_j[-1] if _max_sum < 0: maximum_subarry_endswith_j.append((j, A[j])) else: maximum_subarry_endswith_j.append((_start, _max_sum + A[j])) if maximum_subarry_endswith_j[-1][1] > maximum_subarry[-1]: maximum_subarry = (maximum_subarry_endswith_j[-1][0], j, maximum_subarry_endswith_j[-1][1]) return maximum_subarry数组长度100, 跑1000个100长度的随机的数组, 时间如下:
% python c.py 100 1000 暴力 0.71 分治 0.23 动态规划 0.06 % python c.py 200 1000 暴力 2.57 分治 0.48 动态规划 0.11 % python c.py 400 1000 暴力 10.25 分治 1.08 动态规划 0.23 -
nginx配置中的if条件与querystring配置例子
set $search 0; if ($request_uri ~ "_search"){ set $search 1; } if ($request_uri ~ "_count"){ set $search 1; } if ($arg_ignore_unavailable = true) { set $search "${search}1"; } if ($search = 1) { set $args $args&ignore_unavailable=true; } if ($arg_preference = "") { set $args $args&preference=$upstream_http_django_user; } -
部署superset+clickhouse
我选择使用docker方式安装部署, 虽然中间碰到两个坑, 但对于之后的二次部署或者多次部署,应该还是简单一些.
-
mmap中shared方式锁定的内存能否释放
很多文章都提到 cache中的 shared memory的cache不能被释放, 比如https://linux.cn/article-7310-1.html, 那自然就有一个问题: 如果系统内存用完了, 程序继续通过share memory mmap读取数据, 会发生什么情况?
是老的cache被释放, 还是读取失败?
做了一下测试, 还是会释放的, 只不过不能通过
echo 3 > /proc/sys/vm/drop_caches这种方式释放而已.找一个4G内存的机器做下测试.
写了一段代码, mmap读取一个3G文件的每一页, 这样就会让文件常驻cache了.
echo 3 > /proc/sys/vm/drop_caches之后可以看到cahce没有少, vmtouch也可以看到未释放.然后
cat another-3G-file > /dev/null,通过 vmtouch可以看到老文件已经有page不在cache中了. 而another-3G-file几乎全部在cache. -
golang里面array/slice的内存分配测试1
- 当cap还够用的时候, append不会申请新内存
- cap不够的时候, 会申请一块新内存. buf = append(buf, …), 新得到的buf会是一块新内存,指针是变掉的, 新的cap是之前的两倍(但一定是8的偶数倍, 比如2->8, 10->32)
- newbuf = buf[2:5] 生成slice的时候, newbuf指向buf[2], 他们共用同一块内存, 直到上面2中描述的新内存申请后, 他们会指向不同内存. 不管是buf还是newbuf扩容
- make([]byte, 10)[0:] , len, cap都是10, append会分配新内存.
- make([]byte, 10)[0:0] , len是0, cap是10, append 10 以内不会分配新内存
-
函数中传递指针引起的一个BUG
我是觉得编程里面最烧脑的就是传值和传引用的甄别, 一不小心就会出错.
我是写一个kafka lib https://github.com/childe/healer, producer的类写好了, 然后在此基础上写一个可执行文件, 从stdin输入数据, 然后写入kafka.
简单说一下producer逻辑, 输入1000条之后做为一批数据一起写kafka, 或者是200ms定时器到了就写, 哪怕没有1000条.
但是在测试过程中, 无意间发现, 最终写到kafka的数据是错乱的, 后面写的数据会把前面的数据覆盖掉. 比如先输入 1111111111, 再输入 2222222222, 最后写到kafka的就是两条 2222222222
这就让人很尴尬了…
-
ES中使用mmap存储的索引会锁定内存不释放?
在可用内存不充足的情况下, ES中索引配置如果使用mmapfs, 会导致内存不足, Load飙升.
虽然从发现这个问题到最后确认原因,花了很长时间, 这里长话短说.