算法导论 笔记4 5.2-指示器随机变量
看完之后, 还一时不能熟练理解和应用
5.2-1
正好雇一次的概率是, 最优秀的人出现在第一个的概率, 就是 1/n
雇佣n次的概率是, 所有人正好按从弱到强来面试的概率, 是 1/n!
5.2-2
比如有n个面试者, 第一个出现的肯定要被录取, 设第一个的能力排名是i . 那后面的n-1个人里面, 第 i+1 名之后的这些人, 怎么出现都无所谓, 因为他们肯定不会被录取了. 就看排名在 i 之前的这些人, 一共有 i-1 个人, 他们需要满足且仅需要满足: 排名第1的那个人最先出现, 概率是 1/(i-1)
所以如果第一个人是第2名(概率是1/n), 那么后面录取一个人概率是 1/1,
如果第一个人是第3名(概率是1/n), 那么后面录取一个人概率是 1/2
如果第一个人是第4名(概率是1/n), 那么后面录取一个人概率是 1/3
…
如果第一个人是第n名(概率是1/n), 那么后面录取一个人概率是 1/(n-1)
所以总的概率是 (1+1/2+1/3+…+1/(n-1))/n
我们来模拟一下吧, 看看这个结果对不对.
写一个go的程序, 来输出一下理论上的概率值, 以及模拟出来的”真实”概率. (概率乘了人数 n 然后输出的, 为了和后面提到的欧拉公式做验证)
package main
import (
"flag"
"fmt"
"math/rand"
"time"
)
func P(n int) float32 {
var s float32 = 0.0
for i := 2; i <= n; i++ {
s += 1 / float32(i-1)
}
return s / float32(n)
}
func interview(candidates []int) int {
var (
best = 0
hire_loop_count = 0
)
for _, c := range candidates {
if c > best {
best = c
hire_loop_count++
}
}
return hire_loop_count
}
func generate_candidates(n int) []int {
var (
candidates = make([]int, 0)
exist = make(map[int]bool)
candidate int
)
for len(candidates) < n {
candidate = rand.Intn(5*n) + 1
if _, ok := exist[candidate]; ok {
continue
} else {
exist[candidate] = true
candidates = append(candidates, candidate)
}
}
return candidates
}
var (
loop_count int
N int
)
func init() {
rand.Seed(time.Now().Unix())
flag.IntVar(&loop_count, "loop-count", 100, "")
flag.IntVar(&N, "N", 100, "")
flag.Parse()
}
func main() {
// theory
for n := 2; n < N; n++ {
p := P(n)
fmt.Printf("%d %f %f\n", n, p, p*float32(n))
}
return
// real
var candidates []int
for n := 2; n <= N; n++ {
c := 0
for i := 0; i < loop_count; i++ {
candidates = generate_candidates(n)
if interview(candidates) == 2 {
c++
}
}
fmt.Printf("%d %d %f\n", n, c, float32(c)/float32(loop_count)*float32(n))
}
}
然后用python+plt把图画出来看一下.
import matplotlib.pyplot as plt
import math
X_REAL = []
Y_REAL = []
for l in open('real.txt').readlines():
l = l.strip()
if l:
x, _, y = l.split()
x, y = int(x), float(y)
X_REAL.append(x)
Y_REAL.append(y)
X_THEORY = []
Y_THEORY = []
for l in open('theory.txt').readlines():
l = l.strip()
if l:
x, _, y = l.split()
x, y = int(x), float(y)
X_THEORY.append(x)
Y_THEORY.append(y)
X_Euler = range(2, len(X_THEORY)+2)
Y_Euler = [math.log(x-1) + 0.577 + 1/2/(x-1) for x in X_Euler]
plt.plot(X_REAL, Y_REAL, 'g', X_THEORY , Y_THEORY, 'rs', X_Euler, Y_Euler, 'b^')
plt.show()
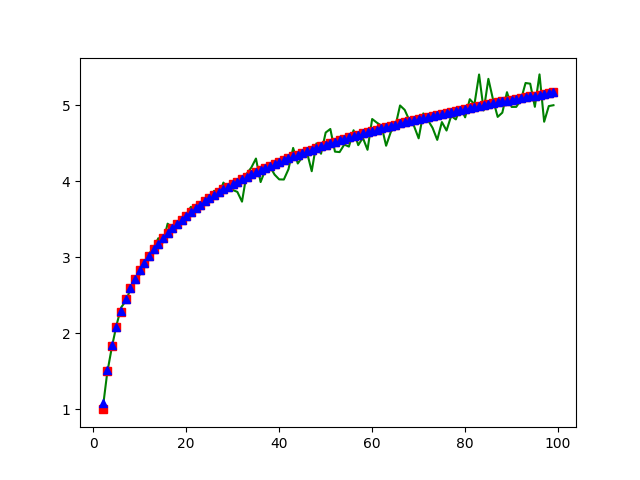
绿色是真实的数据, 红色是理论数据(1+1/2+…+1/(n-1))算出来的, 蓝色是欧拉公式算出来的. 还是符合的不错的. 欧拉公式参考https://zh.wikipedia.org/wiki/调和级数
题外.
因为最近在看机器学习, 感觉这个是一个可以用来学习的例子, 拿tensorflow来学习一下”真实概率”的数据, 看看学习效果怎么样.
from __future__ import print_function
import tensorflow as tf
import numpy as np
X = []
Y = []
for l in open('real.txt').readlines():
l = l.strip()
if l:
x, _, y = l.split()
x, y = float(x), float(y)
X.append(x)
Y.append(y)
X = tf.cast(np.array(X), tf.float32)
Y = tf.cast(np.array(Y), tf.float32)
# Weights_1 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
# Weights_2 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
Weights_3 = tf.Variable(tf.random_uniform([1], -1.0, 1.0), dtype=tf.float32)
biases = tf.Variable(tf.zeros([1]))
# y = Weights_1*X*X + Weights_2*X + biases + Weights_3 * tf.math.log(X)
y = biases + Weights_3 * tf.math.log(X)
loss = tf.reduce_mean(tf.square(y-Y))
# optimizer = tf.train.GradientDescentOptimizer(0.000001)
optimizer = tf.train.AdamOptimizer(0.75)
train = optimizer.minimize(loss)
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
for step in range(100000):
sess.run(train)
if step % 100 == 0:
print(step, sess.run(Weights_3), sess.run(biases), sess.run(loss))
个人感觉效果还算可以吧.
5.2-3
n*(1+2+3+4+5+6)/6
我觉得这个使用指示器变量的想法是很自然的, 反而一般人不会使用”正统”的方法去计算, 所以正统方法就是, n个0的概率0 + n-1个0和1个1的概率1 + … + n个6的概率*6n
5.2-4
每个人拿到自己帽子的概率是 1/n , 所以期望是 1
5.2-5
看第i个数字, 前面有i-1个数字, 每一个比i大的概率是1/2, 所以i前面比i大的数字的个数期望是 (i-1)/2 , 那对i从1取到n, 得到题目答案应该是 西格玛(i-1)/2 i从1到n
验证下看吧.
package main
import (
"fmt"
"math/rand"
"time"
)
func generate_nums(n int) []int {
rand.Seed(time.Now().UnixNano())
var (
nums = make([]int, 0)
exist = make(map[int]bool)
num int
)
for len(nums) < n {
num = rand.Intn(n)
if _, ok := exist[num]; ok {
continue
} else {
exist[num] = true
nums = append(nums, num)
}
}
return nums
}
func inversion_count(nums []int) int {
var count = 0
for i, n1 := range nums {
for _, n2 := range nums[:i] {
if n1 < n2 {
count++
}
}
}
return count
}
func theory(n int) float32 {
var s float32 = 0.0
for i := 1; i <= n; i++ {
s += float32(i-1) / 2
}
return s
}
func main() {
var (
N = 100
count = 1000
)
total := 0
for i := 0; i < count; i++ {
nums := generate_nums(N)
inversion_count := inversion_count(nums)
total += inversion_count
}
fmt.Printf("%f %f\n", theory(N), float32(total)/float32(count))
}
% go run 5.2.5.go
2475.000000 2463.620117